Neil C. Bruce
	Main Page Surface Scattering Capacitance Volume Scattering Polarization Cursos

Numerical Calculations of the scattering of light from randomly rough surfaces with rectangular shaped grooves.

The geometry of the 2D problem is shown below:

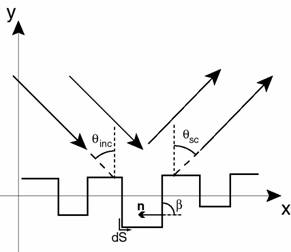
where n is the surface normal, and and are the incident and scattering angles, respectively. We use the Kirchhoff approximation to calculate the scattered intensity for this case. The Kirchhoff approximation can be written as

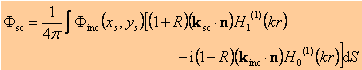
where and are the incident and scattered fields, respectively, R is the Fresnel reflection coefficient, and the functions H( ) are Hankel functions.

The usual formulation of the Kirchhoff approximation uses

where h´(x) is the slope of the surface. Substituting in the equation for the scattered field gives

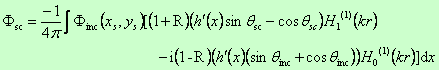
This equation contains the surface slope and so is undefined for the surface shown above, which has infinite slopes. To overcome this problem, we use

which leads to the equation for the scattered field of

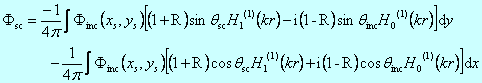
And this equation can be used for the rectangular grooved surface.

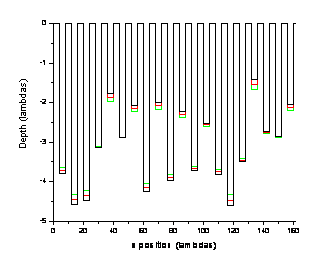
Below we show three different surfaces with constant groove separation and width and a random groove depth with a width of the depth distribution given by the numbers at the side of the graph.

Dh = 1.443l  Dh = 1.590l   Dh = 1.734l

For these three, very similar, surfaces the double scattered intensity in the backscattered direction varies from zero to its maximum value. In the following graphs the backscatter direction is -30°.

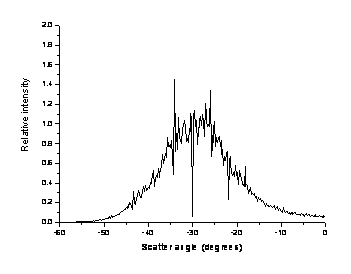	Dh = 1.443l
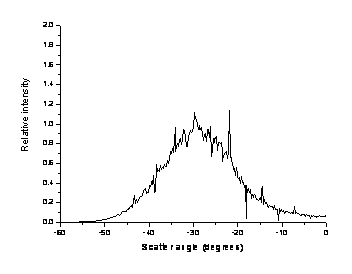	Dh = 1.590l
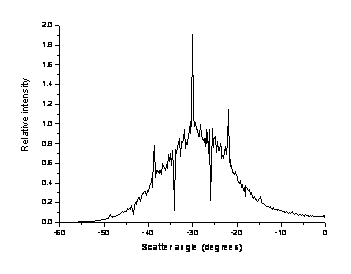	Dh = 1.734l

Publications

• N.C. Bruce, "Scattering from high-sloped surfaces using the Kirchhoff approximation", Proceedings of SPIE, vol. 4780, (2002), 1-6.
• N.C. Bruce, "Scattering from infinitely sloped surfaces by use of the Kirchhoff approximation", Applied Optics, 42, (2003), 2398-2406.
• N.C. Bruce, "Calculations of the light scattered from an infinite-sloped surface using the Kirchhoff approximation", Proceedings of SPIE, vol. 5622, (2004), 1550-1555.
• N.C. Bruce, "Control of the backscattered intensity in random rectangular-groove surfaces with variations in the groove depth", Applied Optics, 44(5), (2005).